1 - Présentation du programme
Tout le code est accessible à l’adresse suivante: https://github.com/Alg0v/fractals
Vous pouvez télécharger le programme pour Windows ici: https://algov.ch/explo_fractales/fractals_windows.zip
Le programme permet de visualiser la fractale de Mandelbrot et les fractales de Julia.
Il est développé en C++ et j’ai mis au point un système de multithreading fonctionnant avec la librairie SDL2 pour que le programme soit le plus réactif possible.
La partie graphique est gérée à l’aide de la librairie SDL2 qui permet d’afficher la fenêtre du programme et de colorier les pixels.
La librairie ImGUI permet d’afficher la fenêtre de menu au démarrage du programme.
En appuyant sur la touche e, on peut choisir d’afficher la fractale de Mandelbrot ou une fractale de Julia.
On peut utiliser la molette pour agrandir une zone qui nous intéresse.
La touche u permet de rafraichir l’écran en cas de bogue d’affichage.
2 - Comment le programme fonctionne
Pour comprendre les paragraphes suivant, il est nécessaire de comprendre ce qu’est un nombre complexe.
Le programme interprète la fenêtre affichée comme un plan complexe.
Il attribue à chaque pixel de la fenêtre un nombre complexe et calcule, à l’aide d’un algorithme si le point appartient ou non à une fractale.
1 - La fractale de Mandelbrot
Pour déterminer si un complexe $z$ appartient à la fractale de Mandelbrot, on utilise le protocole suivant:
On définit une suite: $$\begin{cases} u_0 = 0 \newline \forall n\in\mathbb N_0,\ u_{n+1}=u_n^2 - z \end{cases}$$
Si la suite ne diverge pas, alors ce point appartient à la fractale.
Le programme calcule les termes consécutifs de cette suite jusqu’à que ce qu’un terme ne se trouve plus dans le cercle de rayon $10$ ou qu’il ait calculé trop de termes (généralement $64$).
Plus la suite possède des termes dans ce cercle, moins elle diverge rapidement.
Le programme colore donc l’écran à partir de ces informations.
2 - La fractale de Julia
Le principe utilisé pour générer la fractale de Julia est semblable, on utilise une autre suite cependant :
$$\begin{cases} u_0 = z \newline \forall n\in\mathbb N_0,\ u_{n+1}=u_n^2 - c \end{cases}$$
Avec $c$ une constante complexe qui influence la fractale que l’on obtient.
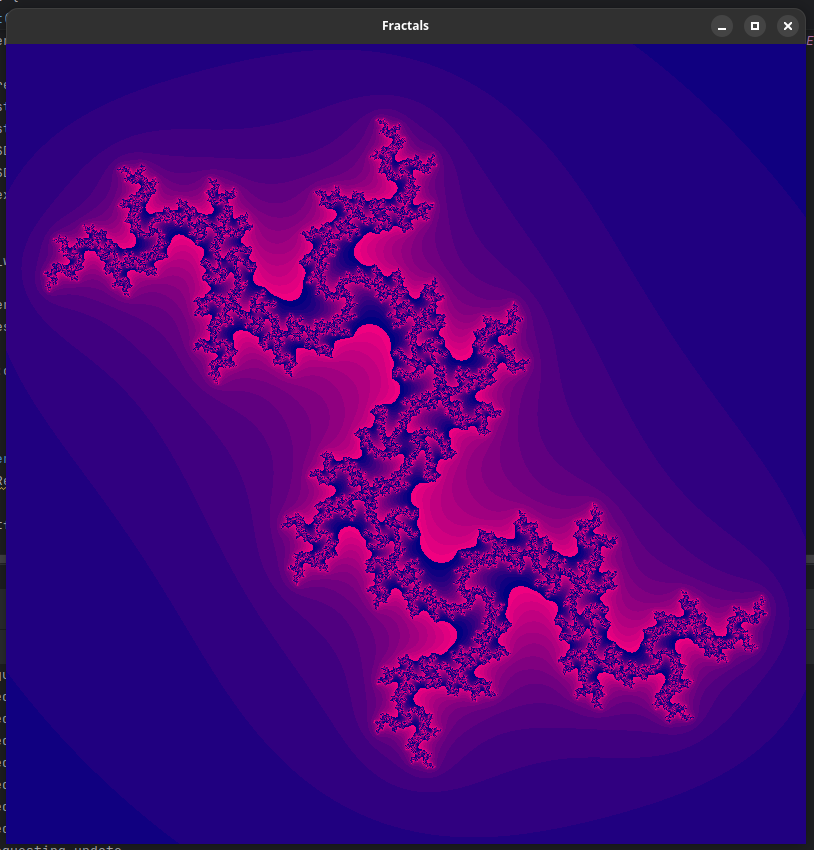
La capture d’écran en haut de l’article montre la fractale associée à $c=0.75i$.
Pour changer la constante que l’on utilise, on peut utiliser le petit menu au démarrage du programme.